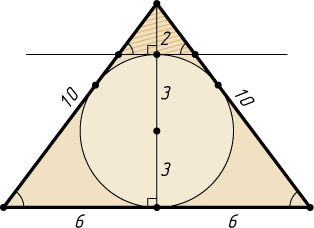
352. К окружности, вписанной в равнобедренный треугольник с основанием 12 и высотой 8, проведена касательная, параллельная основанию. Найдите длину отрезка этой касательной, заключённого между сторонами треугольника.
Ответ. 3.
Указание. Найдите коэффициент подобия отсечённого и данного треугольников.
Решение. Треугольник, отсечённый данной касательной, подобен исходному. Чтобы найти коэффициент подобия, вычтем из высоты исходного треугольника диаметр вписанной окружности, который найдём по формуле площади треугольника (S=pr
, где p
— полупериметр треугольника, r
— радиус вписанной окружности) и разделим эту разность на 8. Получим k=\frac{1}{4}
. Поэтому искомый отрезок равен \frac{1}{4}\cdot12=3
.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.033, с. 161
