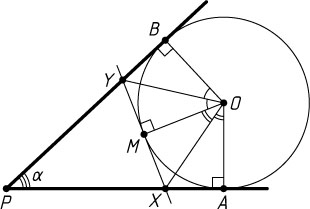
356. Прямые PA
и PB
касаются окружности с центром O
(A
и B
— точки касания). Проведена третья касательная к окружности, пересекающая прямые PA
и PB
в точках X
и Y
. Докажите, что величина угла XOY
не зависит от выбора третьей касательной.
Указание. Угол между радиусами, проведёнными в точки касания, дополняет угол между касательными до 180^{\circ}
.
Решение. Обозначим \angle APB=\alpha
. Пусть M
— точка касания окружности с прямой XY
. Тогда
\angle XOY=\frac{1}{2}\angle AOM+\frac{1}{2}\angle BOM=\frac{1}{2}(\angle AOM+\angle BOM)=
=\frac{1}{2}\angle AOB=\frac{1}{2}(180^{\circ}-\alpha)=90^{\circ}-\frac{\alpha}{2}.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 3.1, с. 58
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 3.1, с. 56
