364. Докажите, что в выпуклый четырёхугольник, суммы противоположных сторон которого равны между собой, можно вписать окружность.
Указание. 1) На отрезке AB
возьмите такую точку T
, для которой AT=AD
, а на отрезке BC
— такую точку S
, для которой CS=CD
. Биссектрисы углов B
, A
и C
являются серединными перпендикулярами к сторонам треугольника DTS
.
2) Пусть AB+CD=BC+AD
и прямые AB
и CD
пересекаются в точке M
. Впишите окружность в треугольник AMB
и докажите, что она вписана в данный четырёхугольник.
Решение. Первый способ. Пусть AB+CD=BC+AD
. Тогда AB-AD=BC-CD
.
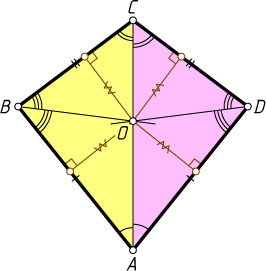
а) Если AB=AD
(рис. 1), то BC=CD
. Поэтому треугольники ABC
и ADC
равны по трём сторонам, значит, диагональ AC
делит пополам углы BAD
и BCD
. Из равенства треугольников ABC
и ADC
и их соответствующих углов ABC
и ADC
следует, что биссектрисы этих углов пересекаются в некоторой точке O
, лежащей на диагонали AC
. Поскольку точка O
лежит на биссектрисе каждого из углов четырёхугольника, то она равноудалена от всех его сторон. Следовательно, O
— центр окружности, вписанной в четырёхугольник ABCD
.
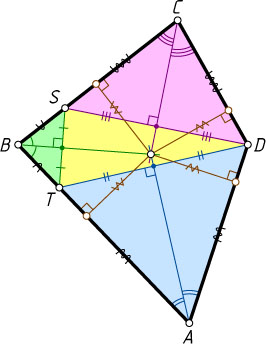
б) Пусть теперь AB\gt AD
(рис. 2). Тогда BC\gt CD
.
На отрезке AB
возьмём такую точку T
, для которой AT=AD
, а на отрезке BC
— такую точку S
, для которой CS=CD
. Поскольку
AT=AD,~CS=CD,~BT=AB-AT=AB-AD=BC-CD=BC-CS=BS,
то треугольники TBS
, ADT
и CDS
— равнобедренные. Биссектрисы их углов при вершинах B
, A
и C
являются серединными перпендикулярами к отрезкам TS
, DT
и DS
соответственно, т. е. серединными перпендикулярами к сторонам треугольника DTS
. Поэтому биссектрисы углов B
, A
и C
пересекаются в одной точке — центре описанной окружности треугольника DTS
. Эта точка равноудалена от всех сторон четырёхугольника ABCD
. Следовательно, она является центром вписанной окружности четырёхугольника ABCD
.
Аналогично для AB\lt AD
.
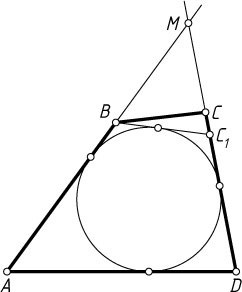
Второй способ. Пусть AB+CD=BC+AD
и прямые AB
и CD
пересекаются в точке M
(рис. 3). Впишем окружность в треугольник AMB
. Пусть она полностью содержится в четырёхугольнике ABCD
. Докажем, что она касается BC
.
Если это не так, то проведём через точку B
касательную к окружности, пересекающую CD
в точке C_{1}
. Тогда
AB+CD=BC+AD~\mbox{и}~AB+C_{1}D=BC_{1}+AD.
Вычитая почленно эти равенства, получим:
CC_{1}+BC_{1}=BC,
что противоречит неравенству треугольника.
Аналогично рассматриваются остальные случаи.
Источник: Ефремовъ Д. Д. Новая геометрiя треугольника. — Одесса, 1902. — с. 106
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — № 87, с. 95
Источник: Пржевальский Е. Собрание геометрических теорем и задач. — М.: Типография Г. Лисснера и Д. Собко, 1909. — № 127, с. 43
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 19, с. 6
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 2, с. 151
Источник: Калинин А. Ю., Терёшин Д. А. Геометрия. 10—11 классы. — М.: МЦНМО, 2011. — с. 596


