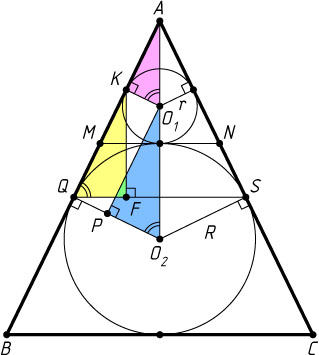
366. Точки M
и N
принадлежат боковым сторонам соответственно AB
и AC
равнобедренного треугольника ABC
, причём MN
параллельно BC
, а в трапецию BMNC
можно вписать окружность. Её радиус равен R
, а радиус окружности, вписанной в треугольник AMN
, равен r
. Найдите:
а) основание BC
;
б) расстояние от точки A
до ближайшей точки касания;
в) расстояние между хордами окружностей, соединяющими точки касания с боковыми сторонами трапеции BMNC
.
Ответ. \frac{2R\sqrt{rR}}{r}
, \frac{2r\sqrt{rR}}{R-r}
, \frac{4rR}{R+r}
.
Указание. Отношение радиусов окружностей, вписанных в подобные треугольники, равно коэффициенту подобия. Рассмотрите подобные треугольники, среди сторон которых есть искомые отрезки.
Решение. а) Треугольник ABC
подобен треугольнику AMN
с коэффициентом \frac{R}{r}
. Следовательно (см. задачу 365),
BC=\frac{R}{r}\cdot MN=\frac{R}{r}\cdot2\sqrt{rR}=\frac{2R\sqrt{rR}}{r}.
б) Пусть O_{1}
и O_{2}
— центры меньшей и большей окружностей соответственно; Q
— точка касания большей окружности с AB
, P
— основание перпендикуляра, опущенного из O_{1}
на O_{2}Q
, K
— точка касания меньшей окружности с AB
. Тогда
O_{2}P=O_{2}Q-PQ=O_{2}Q-O_{1}K=R-r.
Треугольники AKO_{1}
и O_{1}PO_{2}
подобны с коэффициентом \frac{O_{1}K}{O_{2}P}=\frac{r}{R-r}
. Следовательно,
AK=\frac{r}{R-r}\cdot O_{1}P=\frac{r}{R-r}\cdot KQ=\frac{2r\sqrt{rR}}{R-r}.
в) Пусть F
— основание перпендикуляра, опущенного из точки K
на хорду QS
, соединяющую точки касания большей окружности со сторонами AB
и AC
. Из подобия треугольников KFQ
и O_{1}PO_{2}
находим, что
KF=\frac{KQ}{O_{1}O_{2}}\cdot O_{1}P=\frac{2\sqrt{rR}}{R+r}\cdot2\sqrt{rR}=\frac{4rR}{R+r}.