368. Две окружности касаются друг друга внешним образом в точке C
. Радиусы окружностей равны 2 и 7. Общая касательная к обеим окружностям, проведённая через точку C
, пересекается с другой их общей касательной в точке D
. Найдите расстояние от центра меньшей окружности до точки D
.
Ответ. 3\sqrt{2}
.
Указание. Примените свойство высоты прямоугольного треугольника, опущенной на гипотенузу.
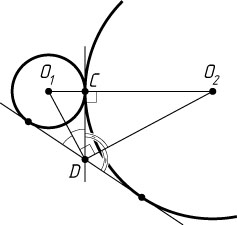
Решение. Пусть O_{1}
и O_{2}
— центры меньшей и большей окружностей. Угол O_{1}DO_{2}
— угол между биссектрисами смежных углов, поэтому \angle O_{1}DO_{2}=90^{\circ}
.
Из прямоугольного треугольника O_{1}DO_{2}
находим, что
O_{1}D^{2}=O_{1}C\cdot O_{1}O_{2}=2\cdot9.
Следовательно, O_{1}D=3\sqrt{2}
.
Источник: Вступительный экзамен на факультет почвоведения МГУ. — 1987, вариант 2, № 4
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 91
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 9.17, с. 68
