369. Теорема Брахмагупты. Диагонали вписанного четырёхугольника перпендикулярны и пересекаются в точке P
. Докажите, что прямая, проходящая через точку P
и перпендикулярная одной из сторон четырёхугольника, делит противоположную сторону пополам.
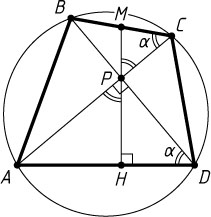
Решение. Пусть H
и M
— точки пересечения данной прямой со сторонами соответственно AD
и BC
данного четырёхугольника ABCD
, PH\perp AD
.
Обозначим \angle ACB=\angle ADB=\alpha
. Тогда
\angle BPM=\angle DPH=90^{\circ}-\alpha,~\angle CPM=90^{\circ}-(90^{\circ}-\alpha)=\alpha=\angle PCM,
значит, треугольник CMP
равнобедренный, PM=CM
. Аналогично PM=BM
. Следовательно, PM
— медиана треугольника BPC
. Что и требовалось доказать.
Примечание. 1. Обратное утверждение также верно: прямая, проходящая через точку P
и середину стороны такого четырёхугольника, перпендикулярна противоположной стороне.
2. См. статью В.Дубровского «Геометрические метаморфозы», Квант, 1997, N6, с.26-30.
Источник: Коксетер Г. С. М., Грейтцер С. Л. Новые встречи с геометрией. — М.: Наука, 1978. — с. 74
Источник: Журнал «Квант». — 1997, № 6, с. 27
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 75, с. 145
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 2.76, с. 39
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 2.79, с. 38
