373. В равнобедренной трапеции лежат две окружности. Одна из них, радиуса 1, вписана в трапецию, а вторая касается двух сторон трапеции и первой окружности. Расстояние от вершины угла, образованного двумя сторонами трапеции, касающимися второй окружности, до точки касания окружностей вдвое больше диаметра второй окружности. Найдите площадь трапеции.
Ответ. \frac{9\sqrt{2}}{2}
.
Указание. Найдите значения тригонометрических функций угла между линией центров двух данных окружностей и боковой стороной трапеции.
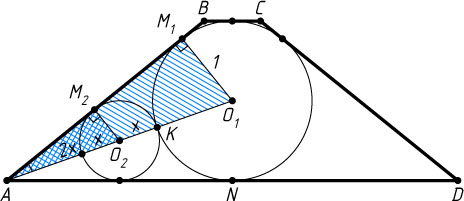
Решение. Пусть O_{1}
и O_{2}
— центры соответственно первой и второй окружности, M_{1}
и M_{2}
— их точки касания с боковой стороной AB
трапеции ABCD
, N
— точка касания первой окружности с основанием AD
, K
— точка касания окружностей, x
— радиус второй окружности.
В треугольнике AO_{2}M_{2}
катет O_{2}M_{2}=x
, гипотенуза AO_{2}=3x
,
\sin\angle BAO_{2}=\frac{1}{3},~\ctg\angle BAO_{2}=2\sqrt{2}.
Из прямоугольного треугольника AO_{1}M_{1}
находим, что
M_{1}A=O_{1}M_{1}\ctg\angle BAO_{1}=2\sqrt{2}.
Поскольку O_{1}M^{2}_{1}=BM_{1}\cdot M_{1}A
(см. задачу 656), то
BM_{1}=\frac{O_{1}M^{2}_{1}}{M_{1}A}=\frac{\sqrt{2}}{4}.
Следовательно, основания трапеции равны 4\sqrt{2}
и \frac{\sqrt{2}}{2}
. Тогда
S_{ABCD}=\frac{4\sqrt{2}+\frac{\sqrt{2}}{2}}{2}\cdot2=\frac{9\sqrt{2}}{2}.
Источник: Вступительный экзамен на факультет почвоведения МГУ. — 1975, вариант 2, № 4
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 99
