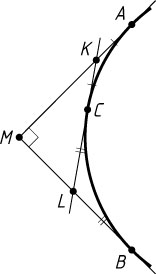
375. Дана окружность радиуса 1. Из внешней точки M
к ней проведены две взаимно перпендикулярные касательные MA
и MB
. Между точками касания A
и B
на меньшей дуге AB
взята произвольная точка C
и через неё проведена третья касательная KL
, образующая с касательными MA
и MB
треугольник KLM
. Найдите периметр этого треугольника.
Ответ. 2.
Указание. Отрезки касательных, проведённых к окружности из одной точки, равны между собой.
Решение. Поскольку KA=KC
и BL=LC
, то
ML+LK+KM=ML+(LC+CK)+KM=
=(ML+LC)+(CK+KM)=(ML+LB)+(AK+KM)=
=MB+AM=1+1=2.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 21(а), с. 30
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 8.13, с. 61
