376. Две окружности радиусов R
и r
касаются сторон данного угла и друг друга. Найдите радиус третьей окружности, касающейся сторон того же угла, и центр которой находится в точке касания двух данных окружностей между собой.
Ответ. \frac{2rR}{r+R}
.
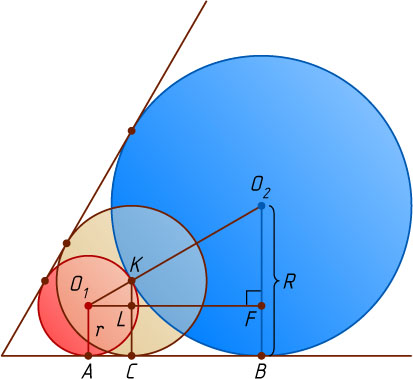
Решение. Пусть окружности радиусов r
и R
касаются одной из сторон угла в точках A
и B
соответственно, а искомая окружность с центром K
касается этой стороны в точке C
. Опустим перпендикуляр O_{1}F
из центра первой окружности на радиус O_{2}B
второй окружности. Пусть L
— точка его пересечения с отрезком O_{1}F
. Тогда прямоугольные треугольники O_{1}LK
и O_{1}FO_{2}
подобны с коэффициентом \frac{O_{1}K}{O_{1}O_{2}}=\frac{r}{R+r}
, следовательно,
KL=O_{2}F\cdot\frac{r}{R+r}=(R-r)\cdot\frac{r}{r+R}=\frac{r(R-r)}{R+r},
KC=KL+LC=KL+O_{1}A=\frac{r(R-r)}{R+r}+r=\frac{2rR}{r+R}.
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 140, с. 19
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 140, с. 17
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 9.22, с. 69
