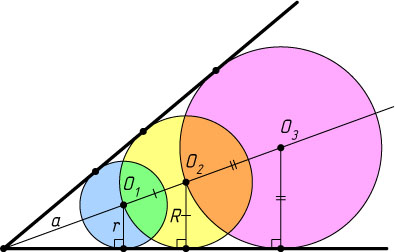
379. В угол вписаны три окружности — малая, средняя и большая. Большая окружность проходит через центр средней, а средняя — через центр малой. Вычислите радиусы средней и большой окружности, если радиус малой равен r
, и расстояние от её центра до вершины угла равно a
.
Ответ. \frac{ar}{a-r}
; \frac{a^{2}r}{(a-r)^{2}}
.
Указание. Рассмотрите подобные прямоугольные треугольники.
Решение. Пусть R
— радиус средней окружности. Проведём радиусы малой и средней окружностей в точки касания с одной из сторон данного угла. Из подобия полученных прямоугольных треугольников следует, что \frac{r}{a}=\frac{R}{R+a}
. Поэтому R=\frac{ar}{a-r}
.
Зная радиус средней окружности, аналогично найдём радиус большой окружности.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.245, с. 175
