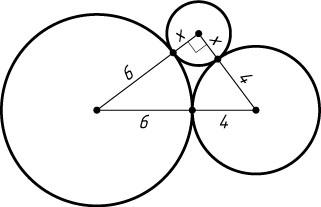
382. Три окружности разных радиусов попарно касаются друг друга внешним образом. Отрезки, соединяющие их центры, образуют прямоугольный треугольник. Найдите радиус меньшей окружности, если радиусы большей и средней равны 6 и 4.
Ответ. 2.
Указание. Линия центров двух касающихся окружностей проходит через их точку касания.
Решение. Пусть x
— радиус меньшей окружности. Стороны получившегося треугольника равны 10, 6+x
и 4+x
.
Поскольку 10 — наибольшая сторона, это гипотенуза. По теореме Пифагора
(x+6)^{2}+(x+4)^{2}=100.
Отсюда находим, что x=2
.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.051, с. 162
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 9.8, с. 67
