383. В равносторонний треугольник вписана окружность. Этой окружности и сторон треугольника касаются три малые окружности. Найдите сторону треугольника, если радиус малой окружности равен r
.
Ответ. 6r\sqrt{3}
.
Указание. Опустите перпендикуляр из центра одной из меньших окружностей на радиус большей окружности, проведённый в точку касания со стороной рассматриваемого угла.
Решение. Пусть R
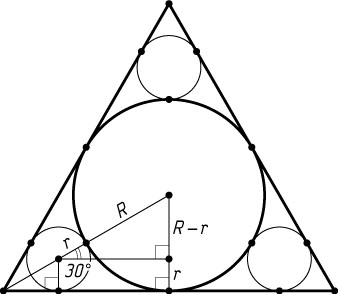
— радиус окружности, вписанной в данный треугольник. Опустим перпендикуляр из центра меньшей окружности на радиус большей окружности, проведённый в точку касания со стороной рассматриваемого угла. Получим прямоугольный треугольник с гипотенузой R+r
, катетом R-r
и углом в 30^{\circ}
, противолежащим этому катету. Поэтому R+r=2(R-r)
. Отсюда находим, что R=3r
. Следовательно, сторона треугольника равна 6r\sqrt{3}
.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.065, с. 163
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 9.13, с. 68
