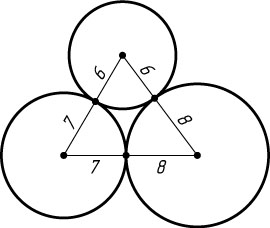
384. Три окружности радиусов 6, 7 и 8 попарно касаются друг друга внешним образом. Найдите площадь треугольника с вершинами в центрах этих окружностей.
Ответ. 84.
Указание. Линия центров двух касающихся окружностей проходит через их точку касания.
Стороны данного треугольника равны 13, 14 и 15. Его площадь найдём по формуле Герона.
Решение. Линия центров двух касающихся окружностей проходит через их точку касания, поэтому стороны треугольника с вершинами в центрах окружностей равны 13, 14 и 15. Пусть S
— площадь треугольника, p
— полупериметр. Тогда p=\frac{1}{2}(13+14+15)=21
. По формуле Герона
S=\sqrt{p(p-13)(p-14)(p-15)}=\sqrt{21(21-13)(21-14)(21-15)}=
=\sqrt{21\cdot8\cdot7\cdot6}=7\cdot3\cdot4=84.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.158, с. 169
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 9.3, с. 67
