385. Даны окружности радиусов r
и R
(R\gt r
). Расстояние между их центрами равно a
(a\gt R+r
). Найдите отрезки общих внешних и общих внутренних касательных, заключённые между точками касания.
Ответ. \sqrt{a^{2}-(R+r)^{2}}
, \sqrt{a^{2}-(R-r)^{2}}
.
Указание. Опустите перпендикуляр из центра одной из окружностей на радиус (или его продолжение) другой окружности, проведённый в точку касания с общей касательной.
Решение. Пусть O_{1}
и O_{2}
— центры окружностей радиусов r
и R
, A
и B
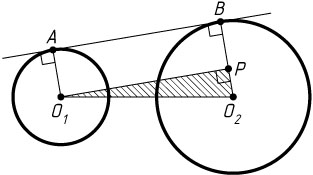
— соответственные точки касания окружностей с общей внешней касательной, C
и D
— с общей внутренней.
Пусть P
— основание перпендикуляра, опущенного из O_{1}
на O_{2}B
. Из прямоугольного треугольника O_{1}PO_{2}
находим, что
O_{1}P=\sqrt{O_{1}O_{2}^{2}-O_{2}P^{2}}=\sqrt{a^{2}-(R-r)^{2}}.
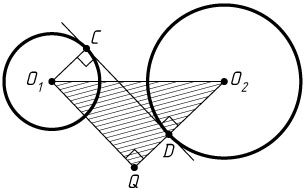
Пусть Q
— основание перпендикуляра, опущенного из O_{1}
на продолжение O_{2}D
. Из прямоугольного треугольника O_{1}QO_{2}
находим, что
O_{1}Q=\sqrt{O_{1}O_{2}^{2}-O_{2}Q^{2}}=\sqrt{a^{2}-(R+r)^{2}}.
Следовательно,
AB=O_{1}P=\sqrt{a^{2}-(R-r)^{2}},~CD=O_{1}Q=\sqrt{a^{2}-(R+r)^{2}}.
Источник: Делоне Б. Н., Житомирский О. К. Задачник по геометрии. — М.—Л.: ОГИЗ, 1949. — № 211, с. 22
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — с. 59

