386. С помощью циркуля и линейки постройте общие касательные к двум данным окружностям.
Указание. Сведите задачу к построению прямоугольного треугольника по гипотенузе и катету (или примените гомотетию).
Решение. Первый способ. Пусть O_{1}
и O_{2}
— центры окружностей радиусов R
и r
(R\gt r
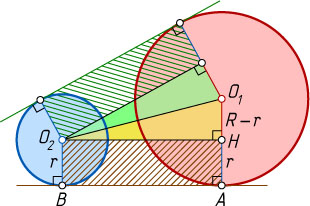
). Предположим, что некоторая прямая касается окружностей в точках A
и B
соответственно (рис. 1), причём эти точки лежат по одну сторону от прямой O_{1}O_{2}
. Опустим перпендикуляр O_{2}H
из центра меньшей окружности на радиус O_{1}A
большей окружности, проведённый в точку касания. Тогда HABO_{2}
— прямоугольник. В прямоугольном треугольнике O_{1}HO_{2}
известны катет O_{1}H=R-r
и гипотенуза O_{1}O_{2}
.
Отсюда вытекает следующее построение. Прямоугольный треугольник O_{1}HO_{2}
строим по катету R-r
и гипотенузе O_{1}O_{2}
. Пересечение продолжения катета O_{1}H
за точку H
с большей окружностью есть искомая точка касания A
. Через точку A
проводим прямую, перпендикулярную O_{1}A
, и опускаем на неё перпендикуляр O_{2}B
из точки O_{2}
.
Поскольку HABO_{2}
— прямоугольник, то
O_{2}B=AH=O_{1}A-O_{1}H=R-(R-r)=r.
Значит, точка B
лежит на окружности с центром O_{2}
, а так как O_{2}B\perp AB
, то прямая AB
— касательная и к этой окружности.
Поскольку возможны ровно два положения точки H
относительно прямой O_{1}O_{2}
, то задача имеет два решения.
Построение в случае, когда R=r
, очевидно.
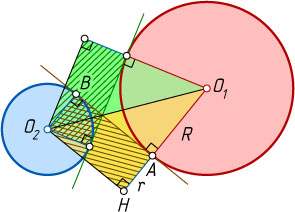
Построение общих внутренних касательных аналогично изложенному (рис. 2). Оно отличается лишь тем, что прямоугольный треугольник O_{1}HO_{2}
строится по гипотенузе O_{1}O_{2}
и катету R+r
(а не R-r
).
Ясно, что построение общих внутренних касательных возможно лишь в случае, когда расстояние между центрами окружностей не меньше суммы радиусов. Если O_{1}O_{2}=r+R
, то общая внутренняя касательная единственна (в этом случае окружности касаются внешним образом).
Второй способ. Пусть R\gt r
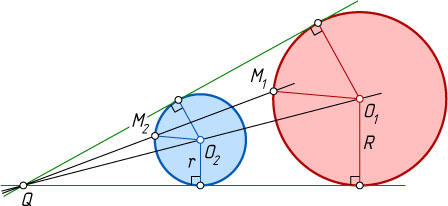
. Найдём центр гомотетии данных окружностей. Для этого проведём произвольный радиус O_{1}M_{1}
первой окружности и параллельный ему радиус O_{2}M_{2}
второй окружности. При этом точки M_{1}
и M_{2}
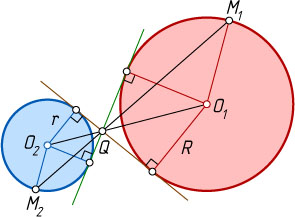
могут лежать либо по одну сторону от прямой O_{1}O_{2}
(рис. 3), либо — по разные (рис. 4).
В каждом из этих случаев искомый центр Q
гомотетии есть точка пересечения прямых M_{1}M_{2}
и O_{1}O_{2}
(в первом случае коэффициент гомотетии равен \frac{R}{r}
, во втором — (-\frac{R}{r}
)).
Поскольку при гомотетии касательная переходит в касательную (прямая, имеющая единственную общую точку с окружностью), то достаточно провести из точки Q
касательную к одной из окружностей. Ясно, что она будет касательной и ко второй.
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — с. 91
Источник: Александров И. И. Сборник геометрических задач на построение. — 19-е изд. — М.: Учпедгиз, 1954. — № 66, с. 44
Источник: Петерсен Ю. Методы и теории для решения геометрических задач на построение, приложенные более чем к 400 задачам. — М.: Типография Э. Лисснера и Ю. Романа, 1892. — № 137, с. 25
Источник: Пойа Д. Математическое открытие. — М.: Наука, 1970. — с. 33



