387. На окружности радиуса r
выбраны три точки таким образом, что окружность оказалась разделённой на три дуги, которые относятся как 3:4:5
. В точках деления к окружности проведены касательные. Найдите площадь треугольника, образованного этими касательными.
Ответ. r^{2}(2\sqrt{3}+3)
.
Указание. Найдите углы треугольника.
Решение. Угловые величины полученных дуг равны
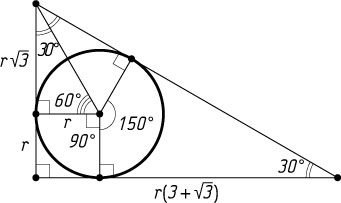
\frac{3}{12}\cdot360^{\circ}=90^{\circ},~\frac{4}{12}\cdot360^{\circ}=120^{\circ},~\frac{5}{12}\cdot360^{\circ}=150^{\circ}.
Поэтому углы треугольника равны 90^{\circ}
, 60^{\circ}
и 30^{\circ}
. Тогда меньший катет равен r(\sqrt{3}+1)
, а больший — r(\sqrt{3}+3)
.
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 36, с. 10
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 36, с. 8
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 8.10, с. 60
