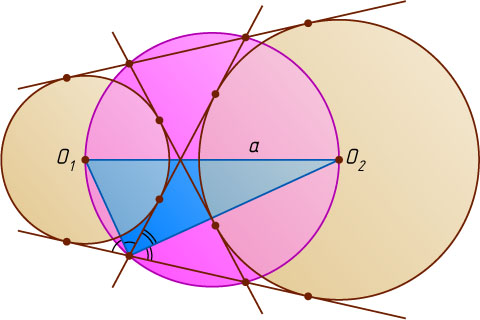
388. Расстояние между центрами непересекающихся окружностей равно a
. Докажите, что точки пересечения общих внешних касательных с общими внутренними касательными лежат на одной окружности и найдите её радиус.
Ответ. \frac{a}{2}
.
Указание. Докажите, что из каждой такой точки отрезок с концами в центрах окружностей виден под прямым углом.
Решение. Поскольку центр окружности вписанной в угол, лежит на биссектрисе этого угла, а угол между биссектрисами смежных углов — прямой, то из каждой точки пересечения общих внешних касательных с общими внутренними отрезок O_{1}O_{2}
с концами в центрах окружностей виден под прямым углом. Значит, каждая такая точка лежит на окружности с диаметром O_{1}O_{2}=a
. Следовательно, радиус окружности равен \frac{a}{2}
.
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 141, с. 19
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 141, с. 17
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 13.20, с. 104
