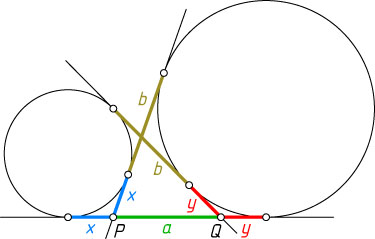
389. Докажите, что отрезок общей внешней касательной к двум окружностям, заключённый между общими внутренними касательными, равен отрезку общей внутренней касательной.
Указание. Отрезки касательных, проведённых из одной точки к окружности, равны между собой.
Решение. Пусть P
и Q
— концы первого отрезка, PQ=a
; x
и y
— отрезки касательных от точки P
до касания с первой окружностью и от точки Q
до точки касания со второй; b
— отрезок общей внутренней касательной.
Отрезки касательных, проведённых из точки P
ко второй окружности, равны между собой: a+y=x+b
. Аналогично для точки Q
: a+x=y+b
. Следовательно, a=b
(и x=y
).
