390. На боковых сторонах PQ
и ST
равнобедренной трапеции PQST
выбраны соответственно точки M
и N
так, что отрезок MN
параллелен основаниям трапеции. Известно, что в каждую из трапеций PMNT
и MQSN
можно вписать окружность. Найдите основания исходной трапеции, если PQ=c
, MN=d
(c\gt2d)
.
Ответ. c-d\pm\sqrt{c(c-2d)}
.
Указание. Трапеции PMNT
и MQSN
подобны.
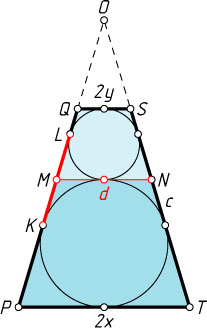
Решение. Первый способ. При гомотетии с центром в точке пересечения прямых PQ
и ST
, переводящей окружность, вписанную в трапецию PMNT
, в окружность, вписанную в трапецию MQSN
, первая трапеция переходит во вторую (рис. 1). Значит, трапеции PMNT
и MQSN
подобны. Обозначим TP=2x
, QS=2y
. Поскольку \frac{TP}{MN}=\frac{MN}{QS}
, то xy=\frac{d^{2}}{4}
.
Если K
и L
— точки касания окружностей со стороной PQ
, то
KL=MN=d,~PQ=PK+KL+LQ=x+y+d.
Отсюда находим, что x+y=c-d
. Следовательно, x
и y
— корни квадратного уравнения
t^{2}-(c-d)t+\frac{d^{2}}{4}=0.
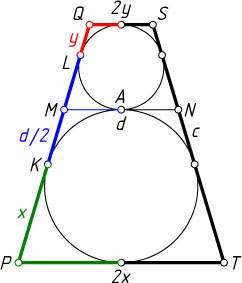
Второй способ. Обозначим TP=2x
, QS=2y
(рис. 2). Пусть K
и L
— точки касания указанных окружностей со стороной PQ
(K
между M
и P
), A
— точка касания окружностей. Тогда
QL=y,~KM=MA=ML=\frac{d}{2},~PK=x.
Если r
и R
— радиусы окружностей, то
r^{2}=\frac{xd}{2},~R^{2}=\frac{yd}{2},~d=KL=2\sqrt{rR}
(см. задачу 365). Поэтому xy=\frac{d^{2}}{4}
. Кроме того,
c=QL+KL+KP=y+d+x,
т. е. x+y=c-d
. Следовательно, x
и y
— корни квадратного уравнения
t^{2}-(c-d)t+\frac{d^{2}}{4}=0.
Источник: Вступительный экзамен на факультет вычислительной математики и кибернетики (ВМК) МГУ. — 1975, вариант 2, № 3
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 247

