391. Дана прямоугольная трапеция. Известно, что некоторая прямая, параллельная основаниям, рассекает её на две трапеции, в каждую из которых можно вписать окружность. Найдите основания исходной трапеции, если её боковые стороны равны c
и d
(c\lt d)
.
Ответ. \frac{d\pm\sqrt{d^{2}-c^{2}}}{2}
.
Указание. Две полученные трапеции подобны.
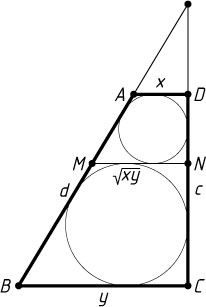
Решение. Пусть указанная прямая пересекает боковые стороны AB=d
и CD=c
трапеции ABCD
соответственно в точках M
и N
. Обозначим искомые основания AD
и BC
через x
и y
соответственно (x\lt y
). При гомотетии с центром в точке пересечения прямых AB
и CD
, переводящей окружность, вписанную в трапецию AMND
, в окружность, вписанную в трапецию MBCN
, первая трапеция переходит во вторую. Значит, трапеции AMND
и MBCN
подобны. Поэтому \frac{AD}{MN}=\frac{MN}{BC}
. Отсюда находим, что MN=\sqrt{xy}
.
Сложив почленно равенства
BC+MN=BM+CN,~MN+AD=AM+DN,
получим, что
x+2\sqrt{xy}+y=c+d,~\mbox{или}~(\sqrt{x}+\sqrt{y})^{2}=c+d.
Кроме того, (y-x)^{2}=d^{2}-c^{2}
.
После упрощения получим линейную систему относительно \sqrt{x}
и \sqrt{y}
:
\syst{\sqrt{y}+\sqrt{x}=\sqrt{d+c}\\\sqrt{y}-\sqrt{x}=\sqrt{d-c}.\\}
Поскольку x\lt y
, то
\sqrt{x}=\frac{\sqrt{d+c}-\sqrt{d-c}}{2},~\sqrt{y}=\frac{\sqrt{d+c}+\sqrt{d-c}}{2}.
Следовательно,
x=\frac{d-\sqrt{d^{2}-c^{2}}}{2},~y=\frac{d+\sqrt{d^{2}-c^{2}}}{2}.
Источник: Вступительный экзамен на факультет вычислительной математики и кибернетики (ВМК) МГУ. — 1975, вариант 1, № 3
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 248
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 26, с. 26
