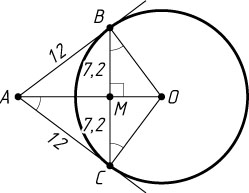
396. Из одной точки проведены к окружности две касательные. Длина каждой касательной равна 12, а расстояние между точками касания равно 14,4. Найдите радиус окружности.
Ответ. 9.
Указание. Угол между данной хордой и радиусом, проведённым в точку касания, равен половине угла между касательными.
Решение. Пусть A
— данная точка, B
и C
— точки касания, O
— центр окружности. Поскольку прямая OA
перпендикулярна отрезку BC
и проходит через его середину M
, то
\angle OCB=\angle OAC,~\sin\angle OAC=\frac{CM}{AC}=\frac{7{,}2}{12}=\frac{3}{5}.
Поэтому \cos\angle OAC=\frac{4}{5}
. Из треугольника OCM
находим, что
OC=\frac{CM}{\cos\angle OCM}=9.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.034, с. 161
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 8.5, с. 60
