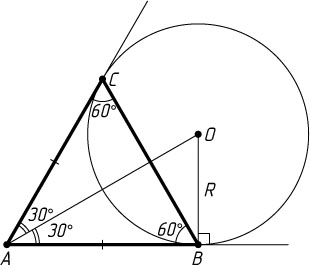
397. Из точки A
проведены две прямые, касающиеся окружности радиуса R
в точках C
и B
, причём треугольник ABC
— равносторонний. Найдите его площадь.
Ответ. \frac{3R^{2}\sqrt{3}}{4}
.
Указание. Выразите AB
через R
.
Решение. Пусть O
— центр окружности. Тогда
\angle OAB=30^{\circ},~AB=R\sqrt{3}.
Следовательно,
S_{\triangle ABC}=\frac{1}{2}AB\cdot AC\sin60^{\circ}=\frac{3R^{2}\sqrt{3}}{4}.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.035, с. 161
