399. Каждая из трёх окружностей радиуса r
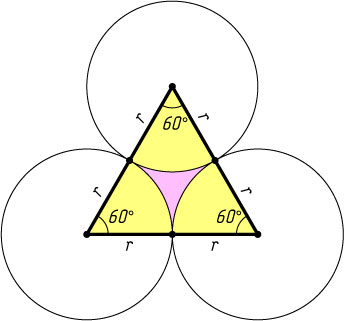
касается двух других. Найдите площадь фигуры, расположенной вне окружностей и ограниченной их дугами, заключёнными между точками касания.
Ответ. r^{2}\left(\sqrt{3}-\frac{\pi}{2}\right)
.
Указание. Искомая площадь равна разности площадей равностороннего треугольника и трёх секторов.
Решение. Искомая площадь равна разности площадей равностороннего треугольника с вершинами в центрах окружностей (его стороны равны 2r
) и трёх секторов данных окружностей.
Площадь каждого сектора составляет шестую часть площади круга. Следовательно, искомая площадь равна
r^{2}\sqrt{3}-\frac{1}{6}\cdot3\pi r^{2}=r^{2}\left(\sqrt{3}-\frac{\pi}{2}\right).
