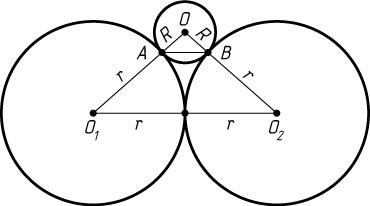
400. Две окружности радиуса r
касаются друг друга. Кроме того, каждая из них касается извне третьей окружности радиуса R
в точках A
и B
соответственно. Найдите радиус r
, если AB=12
, R=8
.
Ответ. 24.
Указание. Рассмотрите подобные треугольники.
Решение. Пусть O_{1}
и O_{2}
— центры окружностей радиуса r
, O
— центр окружности радиуса R
. Тогда треугольники OAB
и OO_{1}O_{2}
подобны. Поэтому
\frac{OA}{OO_{1}}=\frac{AB}{O_{1}O_{2}},~\mbox{или}~\frac{8}{8+r}=\frac{12}{2r}.
Отсюда находим, что r=24
.
Источник: Вступительный экзамен на геологический факультет МГУ. — 1971, № 4, вариант 1
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 9.5, с. 67
