402. Две касающиеся окружности с центрами O_{1}
и O_{2}
касаются внутренним образом окружности радиуса R
с центром O
. Найдите периметр треугольника OO_{1}O_{2}
.
Ответ. 2R
.
Указание. Линия центров двух касающихся окружностей проходит через их точку касания.
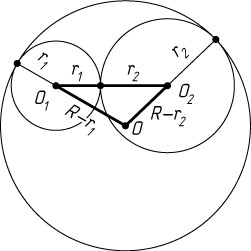
Решение. Пусть r_{1}
и r_{2}
— радиусы окружностей с центрами O_{1}
и O_{2}
соответственно. Линия центров двух касающихся окружностей проходит через точку касания, поэтому
OO_{1}=R-r_{1},~OO_{2}=R-r_{2},~O_{1}O_{2}=r_{1}+r_{2}.
Следовательно,
OO_{1}+OO_{2}+O_{1}O_{2}=R-r_{1}+R-r_{2}+r_{1}+r_{2}=2R.
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 3.19, с. 58
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — Диагностическая работа 2, задача 2
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 2, с. 165
