403. Дана окружность радиуса R
. Четыре окружности равных радиусов касаются данной внешним образом, и каждая из этих четырёх окружностей касается двух других. Найдите радиусы этих четырёх окружностей.
Ответ. \frac{R}{\sqrt{2}-1}
.
Указание. Четырёхугольник с вершинами в центрах четырёх данных равных окружностей — квадрат.
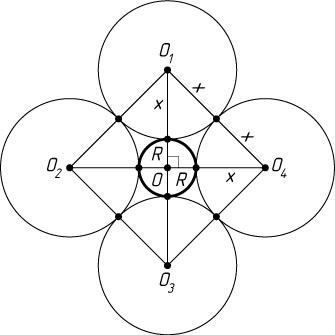
Решение. Пусть R
— радиус данной окружности, x
— радиус остальных окружностей. Обозначим их центры соответственно O
, O_{1}
, O_{2}
, O_{3}
, O_{4}
.
Четырёхугольник O_{1}O_{2}O_{3}O_{4}
— ромб со стороной 2x
. Поскольку его вершины расположены на одинаковом расстоянии от точки O
, то это квадрат. Поэтому 2x=(R+x)\sqrt{2}
. Отсюда находим, что
x=\frac{R}{\sqrt{2}-1}.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.116, с. 116
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 9.7, с. 67
