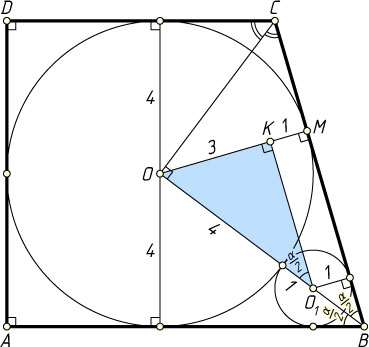
404. В прямоугольной трапеции лежат две окружности. Одна из них, радиуса 4, вписана в трапецию, а вторая, радиуса 1, касается двух сторон трапеции и первой окружности. Найдите площадь трапеции.
Ответ. \frac{196}{3}
.
Указание. Определите положение второй окружности и найдите значения тригонометрических функций половины угла при основании трапеции.
Решение. Пусть O
— центр окружности, вписанной в данную трапецию ABCD
с основаниями AB
и CD
и боковыми сторонами AD
и BC
(AD\lt BC
, DC\lt AB
). Ясно, что вторая окружность касается большей боковой стороны BC
.
Обозначим через \alpha
угол ABC
. Тогда, опустив перпендикуляр O_{1}K
из центра второй окружности на радиус первой, проведённый в точку M
её касания с BC
, найдём:
\sin\frac{\alpha}{2}=\frac{3}{5},~\cos\frac{\alpha}{2}=\frac{4}{5},~\tg\frac{\alpha}{2}=\frac{3}{4}.
Из треугольника BOM
находим, что BM=\frac{16}{3}
. Значит,
CM=3,~BC=\frac{25}{3},
а так как трапеция описанная, то сумма её оснований равна сумме боковых сторон, т. е. 8+\frac{25}{3}=\frac{49}{3}
. Следовательно,
S_{ABCD}=\frac{1}{2}\cdot\frac{49}{3}\cdot8=\frac{196}{3}.
Источник: Вступительный экзамен на факультет почвоведения МГУ. — 1975, вариант 4, № 4
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 100
