407. Точка D
лежит на стороне AC
треугольника ABC
. Окружность радиуса \frac{2}{\sqrt{3}}
, вписанная в треугольник ABD
, касается стороны AB
в точке M
, а окружность радиуса \sqrt{3}
, вписанная в треугольник BCD
, касается стороны BC
в точке N
. Известно, что BM=6
, BN=5
. Найдите стороны треугольника ABC
.
Ответ. AB=BC=AC=8
.
Указание. Найдите косинус угла BDC
и примените теорему косинусов.
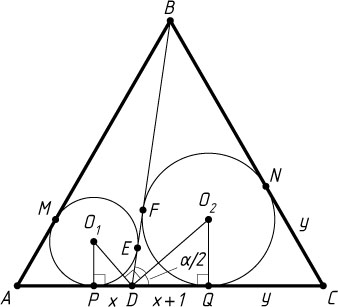
Решение. Пусть O_{1}
и O_{2}
— центры окружностей, P
и Q
— точки их касания со стороной AC
, E
и F
— с отрезком BD
. Обозначим DP=x
. Тогда
DQ=DF=DE+EF=DE+BE-BF=DE+BM-BN=x+1.
Обозначим \angle BDC=\alpha
. Тогда \angle O_{2}DQ=\frac{\alpha}{2}
. Поскольку \angle O_{1}DO_{2}=90^{\circ}
, то \angle O_{1}DP=90^{\circ}-\frac{\alpha}{2}
. Поэтому
DQ=O_{2}Q\ctg\frac{\alpha}{2}=\sqrt{3}\ctg\frac{\alpha}{2},~DP=PO_{1}\tg\frac{\alpha}{2}=\frac{2}{\sqrt{3}}\tg\frac{\alpha}{2},
или
x+1=\sqrt{3}\ctg\frac{\alpha}{2},~x=\frac{2}{\sqrt{3}}\tg\frac{\alpha}{2}.
Перемножив эти равенства почленно, получим уравнение x(x+1)=2
.
Отсюда находим, что x=1
(второй корень не подходит). Поэтому
BD=7,~\tg\frac{\alpha}{2}=\frac{\sqrt{3}}{2},~\cos\alpha=\frac{1}{7}.
Обозначим CQ=CN=y
. По теореме косинусов из треугольника BDC
находим, что
(5+y)^{2}=49+(2+y)^{2}-2\cdot7\cdot(2+y)\cdot\frac{1}{7}.
Откуда y=3
. Аналогично находим, что AP=AM=2
. Следовательно,
AB=AM+MB=2+6=8,~BC=BN+NC=5+3=8,
AC=AP+PD+DQ+CN=2+1+2+3=8.
Источник: Вступительный экзамен в МФТИ. — 1981, билет 3, № 4
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 81-3-4, с. 232
