408. В треугольнике ABC
на стороне AC
взята точка D
так, что окружности, вписанные в треугольники ABD
и BCD
, касаются. Известно, что AD=2
, CD=4
, BD=5
. Найдите радиусы окружностей.
Ответ. \frac{2}{\sqrt{6}}
; \frac{3}{\sqrt{6}}
.
Указание. Примените формулу Герона.
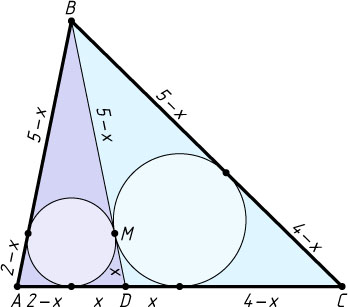
Решение. Пусть M
— точка касания окружностей, DM=x
. Тогда
AB=7-2x,~BC=9-2x.
Выразим через x
площади треугольников ABD
и BCD
по формуле Герона. Отношение площадей равно \frac{AD}{DC}=\frac{1}{2}
. Из полученного уравнения находим, что x=1
.
Радиусы вписанных окружностей найдём, разделив площади треугольников ABD
и BCD
на их полупериметры.
Источник: Вступительный экзамен в МФТИ. — 1981, билет 4, № 4
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 81-4-4, с. 233
