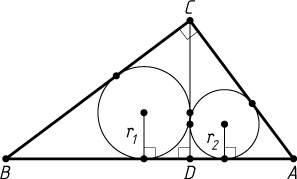
413. Прямоугольный треугольник ABC
разделён высотой CD
, проведённой к гипотенузе, на два треугольника: BCD
и ACD
. Радиусы окружностей, вписанных в эти треугольники, равны 4 и 3 соответственно. Найдите радиус окружности, вписанной в треугольник ABC
.
Ответ. 5.
Указание. Отношение радиусов окружностей, вписанных в подобные треугольники, равно коэффициенту подобия.
Решение. Пусть r
— искомый радиус, r_{1}
и r_{2}
— радиусы данных окружностей. Из подобия треугольников CBD
и ABC
находим, что \frac{r_{1}}{r}=\frac{BC}{AB}
, а из подобия треугольников ACD
и ABC
— \frac{r_{2}}{r}=\frac{AC}{AB}
. Возведём обе части этих равенств в квадрат и сложим почленно полученные равенства. Тогда
\frac{r^{2}_{1}}{r^{2}}+\frac{r^{2}_{2}}{r^{2}}=\frac{BC^{2}}{AB^{2}}+\frac{AC^{2}}{AB^{2}}=1,~r^{2}=r^{2}_{1}+r^{2}_{2}=16+9=25.
Следовательно, r=5
.
Источник: Журнал «Mathematics Magazine». — 1962, том 35, № 5, задача 479, с. 315
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 165, с. 195
Источник: Пржевальский Е. Собрание геометрических теорем и задач. — М.: Типография Г. Лисснера и Д. Собко, 1909. — № 218, с. 94
Источник: Вступительный экзамен в МФТИ. — 1962, билет 7, № 2.
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 62-7-2, с. 93
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 102.76, с. 177
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 11.26, с. 88
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 2.20, с. 24
Источник: Готман Э. Г., Скопец З. А. Решение геометрических задач аналитическим методом: Пособие для учащихся 9—10 кл. — М.: Просвещение, 1979. — № 319(1), с. 49
Источник: Куланин Е. Д., Федин С. Н. Геометрия треугольника в задачах: Экспериментальное учебное пособие для 8—10 кл. школ физико-математического направления. — М.: НИИ школ, 1990. — № 35(1), с. 33
