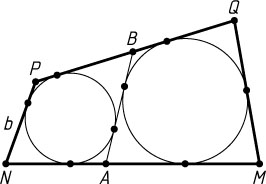
416. В четырёхугольнике MNPQ
расположены две непересекающиеся окружности так, что одна из них касается сторон MN
, NP
, PQ
, а другая — сторон MN
, MQ
, PQ
. Точки B
и A
лежат соответственно на сторонах MN
и PQ
, причём отрезок AB
касается обеих окружностей. Найдите длину стороны MQ
, если NP=b
и периметр четырёхугольника BAQM
больше периметра четырёхугольника ABNP
на величину 2p
.
Ответ. b+p
.
Указание. Суммы противоположных сторон описанного четырёхугольника равны между собой.
Решение. Поскольку четырёхугольники ABMQ
и ABNP
описанные, то
MQ+AB=\frac{1}{2}P_{1},~AB+NP=\frac{1}{2}P_{2},
где P_{1}
и P_{2}
— периметры этих четырёхугольников. Поэтому
MQ-NP=\frac{1}{2}(P_{1}-P_{2})=p.
Отсюда находим, что
MQ=NP+p=b+p.
