418. В треугольнике ABC
сторона BC
равна a
, радиус вписанной окружности равен r
. Найдите радиусы двух равных окружностей, касающихся друг друга, если одна из них касается сторон BC
и BA
, а другая — BC
и CA
.
Ответ. \frac{ar}{a+2r}
.
Указание. Выразите \cos\frac{1}{2}\angle B+\cos\frac{1}{2}\angle C
через r
и a
или рассмотрите подобные треугольники.
Решение. Первый способ. Если x
— искомый радиус, то
x\ctg\frac{1}{2}\angle B+x\ctg\frac{1}{2}\angle C+2x=a,
а так как
r\ctg\frac{1}{2}\angle B+r\ctg\frac{1}{2}\angle C=a,
то
\ctg\frac{1}{2}\angle B+\ctg\frac{1}{2}\angle C=\frac{a}{r},~\frac{ax}{r}+2x=a.
Следовательно, x=\frac{ar}{a+2r}
.
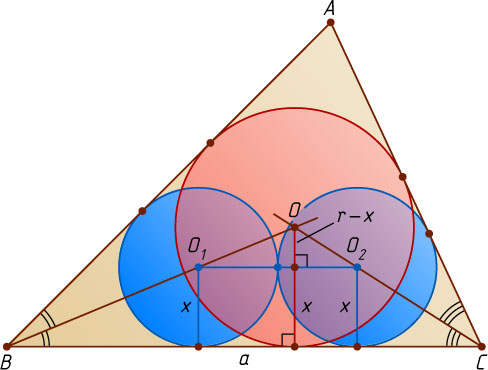
Второй способ. Обозначим через x
искомый радиус. Пусть O_{1}
и O_{2}
— центры указанных равных окружностей. Тогда лучи BO_{1}
и CO_{2}
пересекаются в центре O
вписанной окружности треугольника ABC
.
Отношение высот подобных треугольников OO_{1}O_{2}
и OBC
, проведённых из общей вершины O
, равно отношению соответствующих сторон, т. е.
\frac{r-x}{r}=\frac{2x}{a}.
Следовательно, x=\frac{ar}{a+2r}
.
Источник: Шарыгин И. Ф. Факультативный курс по математике. Решение задач: Учебное пособие для 10 кл. — М.: Просвещение, 1989. — № 240, с. 210
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 157, с. 19
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 9.23, с. 69
