420. Хорда окружности равна 10. Через один конец хорды проведена касательная к окружности, а через другой — секущая, параллельная касательной. Найдите радиус окружности, если внутренний отрезок секущей равен 12.
Ответ. \frac{25}{4}
.
Указание. Диаметр, перпендикулярный хорде, делит её пополам.
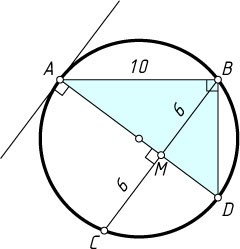
Решение. Пусть AB
— данная хорда. Через точку касания A
проведём диаметр AD
. Пусть M
— точка его пересечения с внутренним отрезком BC
указанной секущей. Проведённый диаметр перпендикулярен касательной, а следовательно, и данной секущей BC
. Поэтому он делит её пополам, т. е. BM=MC=6
.
Из прямоугольного треугольника ABD
(\angle B=90^{\circ}
) находим, что
AB^{2}=AD\cdot AM,~AD=\frac{AB^{2}}{AM}=\frac{100}{8}=\frac{25}{2}.
Значит, радиус окружности равен \frac{25}{4}
.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.014, с. 159
