421. Через концы дуги окружности, содержащей 120^{\circ}
, проведены касательные, и в фигуру, ограниченную этими касательными и данной дугой, вписана окружность. Докажите, что её длина равна длине исходной дуги.
Указание. Докажите, что радиус второй окружности втрое меньше радиуса первой.
Решение. Пусть R
и r
— радиусы данных окружностей. Тогда длина дуги, о которой говорится в условии задачи, равна \frac{1}{3}
длины окружности радиуса R
, т. е. \frac{1}{3}\cdot2\pi R=\frac{2\pi R}{3}
.
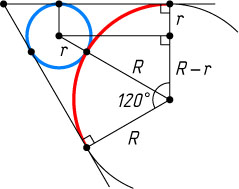
Рассмотрим прямоугольный треугольник с вершинами в центрах данных окружностей и в основании перпендикуляра, опущенного из центра второй окружности на радиус первой окружности, проведённый в точку касания с одной из сторон угла. Его катет, лежащий против угла в 30^{\circ}
, равен половине гипотенузы, т. е. R-r=\frac{1}{2}(R+r)
. Поэтому r=\frac{R}{3}
. Следовательно, длина меньшей окружности также равна \frac{2\pi R}{3}
.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.015, с. 159
