422. Дан квадрат, две вершины которого лежат на окружности радиуса R
, а две другие — на касательной к этой окружности. Найдите диагонали квадрата.
Ответ. \frac{8R\sqrt{2}}{5}
.
Указание. Радиус окружности, проведённый в данную точку касания, есть средняя линия прямоугольной трапеции, одно из оснований которой — сторона квадрата, перпендикулярная касательной.
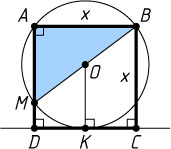
Решение. Пусть A
и B
— вершины квадрата ABCD
, лежащие на окружности радиуса R
и центром O
, D
и C
— на касательной, проведённой к окружности в точке K
, M
— точка пересечения окружности со стороной AD
. Поскольку \angle BAM=90^{\circ}
, то MB
— диаметр окружности, а так как OK
— средняя линия трапеции MDCB
, то \frac{MD+BC}{2}=OK
.
Обозначим через x
сторону квадрата. Из уравнения \frac{MD+x}{2}=R
находим, что MD=2R-x
. Тогда
AM=x-(2R-x)=2x-2R.
По теореме Пифагора
AB^{2}+AM^{2}=BM^{2},~\mbox{или}~x^{2}+(2x-2R)^{2}=4R^{2}.
Из этого уравнения находим, что x=\frac{8R}{5}
. Следовательно, диагональ квадрата равна \frac{8R\sqrt{2}}{5}
.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.023, с. 160
