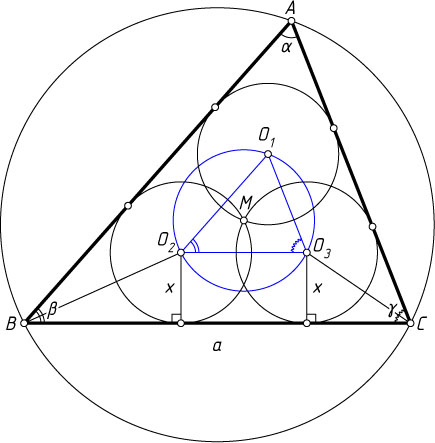
424. В треугольник ABC
помещены три равных окружности, каждая из которых касается двух сторон треугольника. Все три окружности имеют одну общую точку. Найдите радиусы этих окружностей, если радиусы вписанной и описанной окружностей треугольника ABC
равны R
и r
.
Ответ. \frac{rR}{r+R}
.
Указание. Треугольник с вершинами в центрах равных окружностей подобен данному, а радиус его описанной окружности равен радиусу этих окружностей.
Решение. Первый способ. Пусть x
— искомый радиус. Обозначим, BC=a
, \angle A=\alpha
, \angle B=\beta
, \angle C=\gamma
, O_{1}
, O_{2}
, O_{3}
— центры указанных равных окружностей, вписанных в углы A
, B
и C
соответственно, M
— общая точка этих окружностей.
Поскольку x
— радиус окружности, описанной около треугольника O_{1}O_{2}O_{3}
, то
O_{2}O_{3}=2x\sin\angle O_{2}O_{1}O_{3}=2x\sin\alpha,~a=2R\sin\alpha,
\sin\alpha=\frac{a}{2R},~O_{2}O_{3}=\frac{ax}{R}.
С другой стороны,
x\ctg\frac{\beta}{2}+x\ctg\frac{\gamma}{2}+O_{2}O_{3}=a,
r\ctg\frac{\beta}{2}+r\ctg\frac{\gamma}{2}=a,~\mbox{или}~\ctg\frac{\beta}{2}+\ctg\frac{\gamma}{2}=\frac{a}{r}.
Поэтому \frac{ax}{r}+\frac{ax}{R}=a
. Следовательно, x=\frac{rR}{r+R}
.
Второй способ. Будем считать известным, что O_{2}O_{3}=\frac{ax}{R}
(см. первый способ).
Лучи BO_{2}
и CO_{3}
пересекаются в центре O
вписанной окружности треугольника ABC
. Высоты подобных треугольников OO_{2}O_{3}
и OBC
, проведённые из общей вершины O
, относятся как основания этих треугольников. Поэтому
\frac{r-x}{r}=\frac{O_{2}O_{3}}{a}=\frac{x}{R}.
Отсюда находим, что x=\frac{rR}{R+r}
.
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 162, с. 21
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 162, с. 19

