425. В окружности радиуса R
проведена хорда, равная \frac{R}{2}
. Через один конец хорды проведена касательная к окружности, а через другой — секущая, параллельная касательной. Найдите расстояние между касательной и секущей.
Ответ. \frac{R}{8}
.
Указание. Проведите диаметр через точку касания.
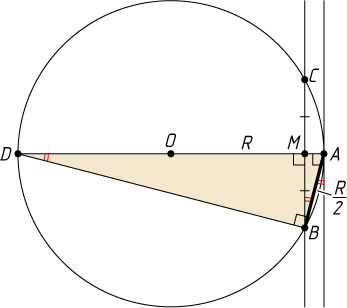
Решение. Пусть AB
— данная хорда, BC
— отрезок данной секущей внутри окружности. Проведём диаметр AD
через точку касания A
. Тогда BC\perp AD
и CM=MB
, где M
— точка пересечения AD
и BC
.
Из прямоугольного треугольника ABD
(\angle B=90^{\circ}
) находим, что
AM\cdot AD=AB^{2},~AM=\frac{AB^{2}}{AD}=\frac{\frac{R^{2}}{4}}{2R}=\frac{R}{8}.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.059, с. 162
