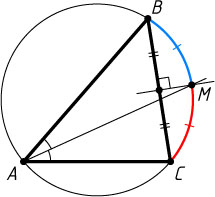
430. Точки A
, B
и C
расположены на окружности. Биссектриса угла BAC
пересекает окружность в точке M
. Докажите, что треугольник BMC
— равнобедренный.
Решение. Вписанные углы MBC
и MAC
опираются на одну и ту же дугу, поэтому они равны (см. задачу 1). Аналогично равны углы MCB
и MAB
, а так как AM
— биссектриса угла BAC
, то \angle MBC=\angle MCB
. Следовательно, треугольник BMC
— равнобедренный.
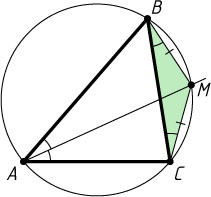
Примечание. Доказанное утверждение равносильно следующему: биссектриса вписанного угла проходит через середину дуги, на которую он опирается.
Из доказанного утверждения также следует, что биссектриса угла A
и серединный перпендикуляр к стороне BC
треугольника ABC
пересекаются на его описанной окружности.
Верно также и следующее утверждение. Биссектриса внешнего угла A
и серединный перпендикуляр к стороне BC
треугольника ABC
, пересекаются на описанной окружности этого треугольника (в середине дуги BAC
).