431. В круге с центром O
хорда AB
пересекает радиус OC
в точке D
, причём \angle CDA=120^{\circ}
. Найдите радиус окружности, касающейся отрезков AD
, DC
и дуги AC
, если OC=2
, OD=\sqrt{3}
.
Ответ. 2\sqrt{21}-9
.
Указание. Линия центров двух касающихся окружностей проходит через их точку касания.
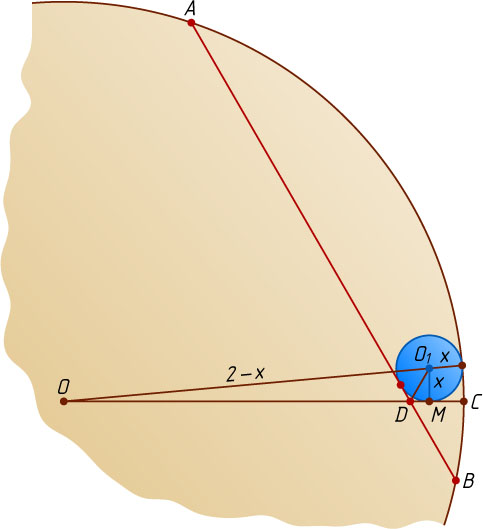
Решение. Пусть x
— радиус искомой окружности, O_{1}
— её центр, M
— точка касания с отрезком DC
. В прямоугольном треугольнике OO_{1}M
известно, что
O_{1}M=x,~OM=OD+DM=\sqrt{3}+\frac{x}{\sqrt{3}},~OO_{1}=2-x.
По теореме Пифагора
OO^{2}_{1}=OM^{2}+O_{1}M^{2},~\mbox{или}~(2-x)^{2}=\left(\sqrt{3}+\frac{x}{\sqrt{3}}\right)^{2}+x^{2}.
Отсюда находим, что x=2\sqrt{21}-9
.
Источник: Вступительный экзамен на филологический факультет МГУ. — 1989, № 4, вариант 1
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 9.37, с. 70
