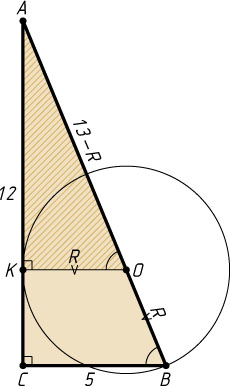
432. Окружность касается большего катета прямоугольного треугольника, проходит через вершину противолежащего острого угла и имеет центр на гипотенузе треугольника. Найдите радиус окружности, если катеты равны 5 и 12.
Ответ. \frac{65}{18}
.
Указание. Расстояние от вершины меньшего острого угла до центра окружности равно разности гипотенузы и радиуса окружности.
Решение. Пусть центр O
окружности лежит на гипотенузе AB
, BC=5
, AC=12
. Поскольку AB=\sqrt{25+144}=13
, то \cos\angle ABC=\frac{5}{13}
.
Если K
— точка касания окружности с катетом AC
, то
OK=AO\cos\angle ABC,~\mbox{или}~R=\frac{5(13-R)}{13},
где R
— искомый радиус. Отсюда находим, что R=\frac{65}{18}
. (Это же уравнение можно получить, рассматривая подобные треугольники AKO
и ACB
.)
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.046, с. 162
