433. Окружность радиуса r
касается некоторой прямой в точке M
. На этой прямой по разные стороны от M
взяты точки A
и B
, причём MA=MB=a
. Найдите радиус окружности, проходящей через точки A
и B
и касающейся данной окружности.
Ответ. \frac{a^{2}+4r^{2}}{4r}
.
Указание. Линия центров двух касающихся окружностей проходит через их точку касания.
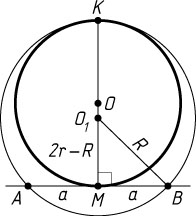
Решение. Пусть R
— радиус искомой окружности, O_{1}
— её центр, K
— точка касания окружностей (касание внутреннее), O
— центр данной окружности. Тогда MO_{1}=|KM-O_{1}K|=|2r-R|
.
Поскольку треугольник MBO_{1}
прямоугольный, то
BO^{2}_{1}=MO^{2}_{1}+MB^{2},~\mbox{или}~R^{2}=(2r-R)^{2}+a^{2}.
Отсюда находим, что
R=\frac{a^{2}+4r^{2}}{4r}.
Источник: Шарыгин И. Ф. Факультативный курс по математике. Решение задач: Учебное пособие для 10 кл. — М.: Просвещение, 1989. — № 112, с. 200
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 68, с. 10
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 9.18, с. 68
