434. Дан ромб со стороной a
и острым углом \alpha
. Найдите радиус окружности, проходящей через две соседние вершины ромба и касающейся противоположной стороны ромба или её продолжения.
Ответ. \frac{a(1+4\sin^{2}\alpha)}{8\sin\alpha}
.
Указание. Радиус окружности, описанной около треугольника, равен стороне треугольника, делённой на удвоенный синус противолежащего угла.
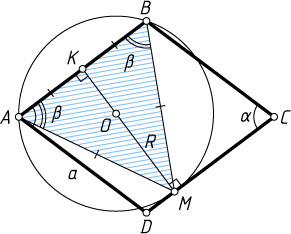
Решение. Пусть R
— радиус окружности, проходящей через вершины A
и B
ромба ABCD
(\angle A=\alpha
) и касающейся прямой DC
в точке M
, K
— середина AB
. Тогда MK=a\sin\alpha
.
Обозначим \angle MAB=\beta
. Тогда
\tg\beta=\frac{KM}{AK}=\frac{a\sin\alpha}{\frac{a}{2}}=2\sin\alpha,~AM=\frac{AK}{\cos\beta}=\frac{a}{2\cos\beta}.
Отсюда находим, что
R=\frac{AM}{2\sin\beta}=\frac{a}{4\sin\beta\cos\beta}=\frac{a}{2\sin2\beta},
а так как
\sin2\beta=\frac{2\tg\beta}{1+\tg^{2}\beta}=\frac{4\sin\alpha}{1+4\sin^{2}\alpha},
то
R=\frac{a(1+4\sin^{2}\alpha)}{8\sin\alpha}.
Источник: Шарыгин И. Ф. Факультативный курс по математике. Решение задач: Учебное пособие для 10 кл. — М.: Просвещение, 1989. — № 110, с. 200
