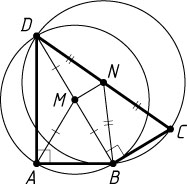
435. В четырёхугольнике ABCD
известны углы: \angle DAB=90^{\circ}
, \angle DBC=90^{\circ}
. Кроме того, DB=a
, DC=b
. Найдите расстояние между центрами двух окружностей, одна из которых проходит через точки D
, A
, B
, а другая — через точки B
, C
, D
.
Ответ. \frac{\sqrt{b^{2}-a^{2}}}{2}
.
Указание. Центр окружности, описанной около прямоугольного треугольника, совпадает с серединой гипотенузы.
Решение. Центр окружности, проходящей через точки D
, A
и B
есть середина M
отрезка DB
; центр окружности, проходящей через точки B
, C
и D
— середина N
отрезка DC
; MN
— средняя линия треугольника DBC
. Следовательно,
MN=\frac{1}{2}BC=\frac{\sqrt{DC^{2}-DB^{2}}}{2}=\frac{\sqrt{b^{2}-a^{2}}}{2}.
Источник: Шарыгин И. Ф. Факультативный курс по математике. Решение задач: Учебное пособие для 10 кл. — М.: Просвещение, 1989. — № 98, с. 199
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 53, с. 9
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 3.6, с. 23
