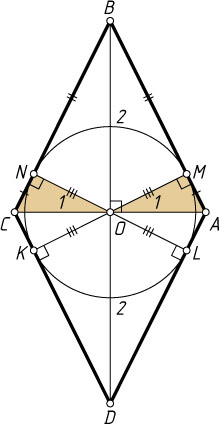
436. Выпуклый четырёхугольник ABCD
описан вокруг окружности с центром в точке O
, при этом AO=OC=1
, BO=OD=2
. Найдите периметр четырёхугольника ABCD
.
Ответ. 4\sqrt{5}
.
Указание. Данный четырёхугольник — ромб.
Решение. Пусть M
, N
, K
и L
— точки касания окружности со сторонами AB
, BC
, CD
, AD
соответственно.
Треугольники AMO
и CNO
равны по гипотенузе и катету, поэтому AM=CN
, а так как BM=BN
, то AB=BC
. Аналогично BC=CD=AD
. Тогда данный четырёхугольник — ромб, а O
— точка пересечения его диагоналей. Значит,
AB=\sqrt{AO^{2}+BO^{2}}=\sqrt{5}.
Следовательно, периметр ромба равен 4\sqrt{5}
.
