438. Дана окружность с центром в точке O
и радиусом 2. Из конца отрезка OA
, пересекающегося с окружностью в точке M
, проведена касательная AK
к окружности, \angle OAK=60^{\circ}
. Найдите радиус окружности, касающейся отрезков AK
, AM
и дуги MK
.
Ответ. 2-\frac{4}{3}\sqrt{2}
.
Указание. Линия центров двух касающихся окружностей проходит через их точку касания.
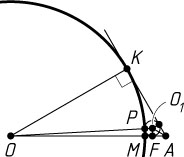
Решение. Пусть O_{1}
— центр искомой окружности, F
— точка касания окружности с отрезком AM
, P
— с дугой MK
, x
— искомый радиус. Тогда
OF=OA-AF=\frac{OK}{\sin60^{\circ}}-FO_{1}\ctg30^{\circ}=\frac{4}{\sqrt{3}}-\frac{3x}{\sqrt{3}}=\frac{4-3x}{\sqrt{3}},
OO_{1}=OP+PO_{1}=2+x.
В прямоугольном треугольнике OFO_{1}
имеем:
OO^{2}_{1}=OF^{2}+O_{1}F^{2},~\mbox{или}~(2+x)^{2}=\frac{(4-3x)^{2}}{3}+x^{2}.
Из этого уравнения находим, что
x=2-\frac{4}{3}\sqrt{2}~\mbox{или}~x=2+\frac{4}{3}\sqrt{2}.
Поскольку 2+\frac{4}{3}\sqrt{2}\gt2
, то условию задачи удовлетворяет только первый корень.
Источник: Вступительный экзамен на биологический факультет МГУ. — 1978, вариант 1, № 3
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 51
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 137, с. 17
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 9.36, с. 70
