439. Радиус OM
окружности с центром в точке O
и хорда KQ
пересекаются в точке A
. Отрезки OM
и OA
равны соответственно r
и a
, \angle KAM=\alpha
(\alpha\lt90^{\circ}
). Найдите радиус окружности, касающейся отрезков AK
, AM
и дуги MK
.
Ответ. \tg^{2}\frac{\alpha}{2}\left(\frac{\sqrt{r^{2}+ar\sin\alpha}}{\sin\frac{\alpha}{2}}-a\ctg\frac{\alpha}{2}-r\right)
.
Указание. Линия центров двух касающихся окружностей проходит через их точку касания.
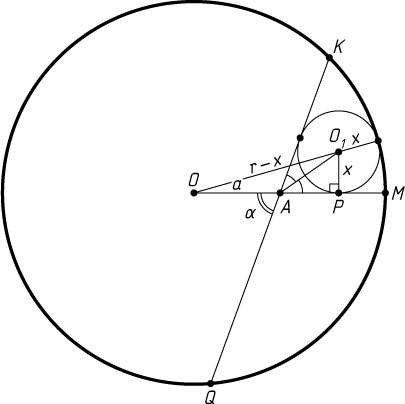
Решение. Пусть O_{1}
— центр искомой окружности, P
— её точка касания с отрезком AM
, x
— её радиус. Тогда
OP=OA+AP=OA+PO_{1}\ctg\frac{\alpha}{2}=a+x\ctg\frac{\alpha}{2},
OO_{1}=r-x.
B
прямоугольном треугольнике OPO_{1}
известно, что
OO^{2}_{1}=OP^{2}+PO^{2}_{1},~\mbox{или}~(r-x)^{2}=\left(a+x\ctg\frac{\alpha}{2}\right)^{2}+x^{2}.
Положительный корень этого уравнения и есть искомый радиус.
Источник: Вступительный экзамен на биологический факультет МГУ. — 1978, вариант 2, № 3
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 52
