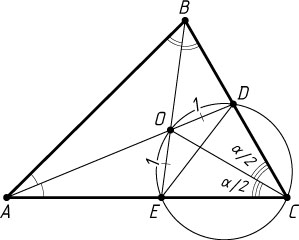
440. В треугольнике ABC
проведены биссектрисы AD
и BE
, пересекающиеся в точке O
. Известно, что отрезок OE=1
, а вершина C
лежит на окружности, проходящей через точки E
, D
и O
. Найдите стороны и углы треугольника EDO
.
Ответ. 1; 1; \sqrt{3}
; 120^{\circ}
; 30^{\circ}
; 30^{\circ}
.
Указание. CO
— биссектриса угла ACB
.
Решение. Поскольку биссектрисы треугольника пересекаются в одной точке, то CO
— биссектриса угла ACB
. Поэтому OD=OE=1
.
Обозначим \angle ACB=\alpha
. Тогда
\angle DOE=\angle AOB=180^{\circ}-\angle OAB-\angle OBA=180^{\circ}-\frac{1}{2}\angle A-\frac{1}{2}\angle B=
=180^{\circ}-\frac{1}{2}(\angle A+\angle B)=180^{\circ}-\frac{1}{2}(180^{\circ}-\angle ACB)=90^{\circ}+\frac{\alpha}{2}.
Поскольку четырёхугольник CEOD
— вписанный, то
\angle ECD+\angle DOE=180^{\circ},~\mbox{или}~\alpha+\left(90^{\circ}+\frac{\alpha}{2}\right)=180^{\circ}.
Отсюда находим, что \alpha=60^{\circ}
. Следовательно,
\angle DOE=120^{\circ},~\angle DEO=\angle EDO=30^{\circ},~DE=\sqrt{3}.
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 1969, № 2, вариант 3
Источник: Журнал «Квант». — 1970, № 2, с. 50, задача 2
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 218, с. 25
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 13.21, с. 104
