441. Через точку A
окружности радиуса 10 проведены две взаимно перпендикулярные хорды AB
и AC
. Вычислите радиус окружности, касающейся данной окружности и построенных хорд, если AB=16
.
Ответ. 8.
Указание. Опустите перпендикуляры из центров обеих окружностей на хорду AB
и рассмотрите полученную прямоугольную трапецию.
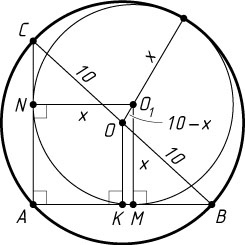
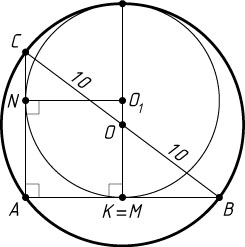
Решение. Пусть O_{1}
— центр искомой окружности, x
— её радиус, M
и N
— точки касания с хордами AB
и AC
, O
— центр данной окружности, K
— середина AB
.
Из прямоугольного треугольника ABC
находим, что AC=12
. Обозначим AM=AN=x
. Тогда стороны прямоугольной трапеции OO_{1}MK
равны:
MO_{1}=AN=x,~OK=\frac{1}{2}AC=6,~MK=|AM-AK|=|8-x|,~OO_{1}=10-x.
По теореме Пифагора
(6-x)^{2}+(8-x)^{2}=(10-x)^{2}.
Отсюда находим, что x=8
.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.255 с. 176
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 8.28, с. 62

