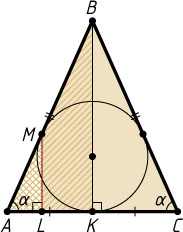
442. В равнобедренный треугольник ABC
с основанием AC
вписана окружность, которая касается боковой стороны AB
в точке M
. Через точку M
проведён перпендикуляр ML
к стороне AC
треугольника ABC
(точка L
— основание этого перпендикуляра). Найдите величину угла BCA
, если известно, что площадь треугольника ABC
равна 1, а площадь четырёхугольника LMBC
равна s
.
Ответ. \arccos\sqrt{2(1-s)}
.
Указание. Треугольник AML
подобен треугольнику ABK
с коэффициентом \cos\alpha
.
Решение. Обозначим искомый угол через \alpha
. Пусть K
— точка касания вписанной окружности со стороной AC
. Тогда K
— середина AC
. Треугольники AML
и ABK
подобны. Поэтому
1-s=S_{\triangle AML}=\left(\frac{AL}{AK}\right)^{2}S_{\triangle ABK}=\frac{1}{2}\left(\frac{AL}{AM}\right)^{2}=\frac{1}{2}\cos^{2}\alpha.
Следовательно, \cos^{2}\alpha=2(1-s)
.
Источник: Вступительный экзамен на химический факультет МГУ. — 1980, вариант 1, № 4
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — № 4, с. 43
