443. В четырёхугольник ABCD
можно вписать и вокруг него можно описать окружность. Диагонали этого четырёхугольника взаимно перпендикулярны. Найдите его площадь, если радиус описанной окружности равен R
и AB=2BC
.
Ответ. \frac{8}{5}R^{2}
.
Указание. 1. Во вписанном четырёхугольнике со взаимно перпендикулярными диагоналями расстояние от центра описанной окружности до одной из сторон равно половине противоположной стороны.
2. Поскольку в четырёхугольник можно вписать окружность, то суммы его противоположных сторон равны, а так как диагонали четырёхугольника перпендикулярны, то равны и суммы квадратов его противоположных сторон (см. задачу 1344).
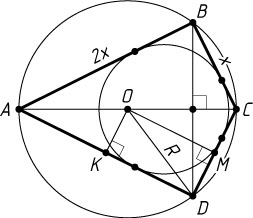
Решение. Первый способ. Обозначим BC=x
. Тогда AB=2x
. Пусть O
— центр описанной окружности, K
и M
— середины AD
и DC
. Тогда
OK=\frac{1}{2}BC=\frac{x}{2},~OM=\frac{1}{2}AB=x,
AD=2DK=\sqrt{R^{2}-\frac{x^{2}}{4}},~CD=2MD=2\sqrt{R^{2}-x^{2}}.
Поскольку AB+CD=BC+AD
, то
2x+2\sqrt{R^{2}-x^{2}}=x+2\sqrt{R^{2}-\frac{x^{2}}{4}}.
Отсюда находим, что
x=\frac{2R}{\sqrt{5}},~AB=\frac{4R}{\sqrt{5}},~AD=\frac{4R}{\sqrt{5}},~BC=\frac{2R}{\sqrt{5}},~CD=\frac{2R}{\sqrt{5}}.
Поэтому AC
— биссектриса угла BCD
и \angle ABC=90^{\circ}
. Следовательно, искомая площадь равна удвоенной площади треугольника ABC
, т. е. \frac{8}{5}R^{2}
.
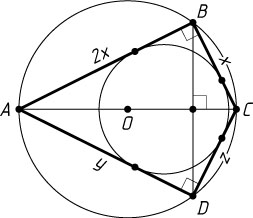
Второй способ. Обозначим BC=x
, AB=2x
, AD=y
, CD=z
. Поскольку в четырёхугольник можно вписать окружность, то суммы его противоположных сторон равны, а так как диагонали четырёхугольника перпендикулярны, то равны и суммы квадратов его противоположных сторон (см. задачу 1344). Тогда
\syst{x+y=2x+z\\x^{2}+y^{2}=4x^{2}+z^{2}\\}~\Leftrightarrow~\syst{x=y-z\\3x^{2}=y^{2}-z^{2}\\}~\Leftrightarrow~\syst{x=y-z\\3x^{2}=(y-z)(y+z)\\}~\Leftrightarrow
\Leftrightarrow~\syst{x=y-z\\3x^{2}=x(y+z)\\}~\Leftrightarrow~\syst{x=y-z\\3x=y+z\\}~\Leftrightarrow~\syst{y=2x\\z=x.\\}
Поэтому BC=DC
и BA=DA
, т. е. точки A
и C
равноудалены от концов отрезка BD
. Значит, прямая AC
— серединный перпендикуляр к хорде BD
описанной окружности четырёхугольника ABCD
. Следовательно, AC
— диаметр этой окружности, \angle ABC=\angle ADC=90^{\circ}
.
По теореме Пифагора
BC^{2}+AB^{2}=AC^{2},~\mbox{или}~x^{2}+4x^{2}=4R^{2},
откуда x^{2}=\frac{4}{5}R^{2}
. Следовательно,
S_{ABCD}=2S_{\triangle ABC}=2\cdot\frac{1}{2}BC\cdot AB=2x^{2}=\frac{8}{5}R^{2}.
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 1971, № 5, вариант 1
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 11.38, с. 89

